有关染色问题是否有通解的证明

导语：有关染色问题是否有通解的证明一文来源于网友上传，不代表本站观点，若需要原创文章可咨询客服老师，欢迎参考。

任何整体陆地板块均可视作由其中任何一国，以每个邻国作为单位自外扩展而成，依次国家为a1、a2、……an，颜色为1、2、3，4遵循以下原则涂色。

1、一旦一国家边界被完全包围，这以后它将不会再有任何新增邻国，同时它的现有邻国也已经全部涂色完毕，因此该国不会对接下来的涂色产生任何影响，出于简化分析的需要将该国视作“消失”。

2、新增国家与原板块有两段以上不连续边界时，这时分段国界空白区域必然会产生的国家，改为优先扩展空白区域国家，至于不连续边界邻国则会在后面涂色，即只扩展连续边界国家。

3、非必要不使用4颜色。

4、先给原有国家涂色后增加新国家只是为分析简化的需要，真实情况是地图上一开始就是客观存在的，预先的涂色是考虑了所有可能情况后多个可选颜色中的一个，但实际地图只有一种情况，所以允许在发现不符合地图实际情况后，在保证规则自治的前提下修改原有颜色。

5、一国如同时在板块边缘拥有两段以上不连续的边界，则客观上在内部形成与整体板块隔绝的封闭区域，封闭区域内按照与该国关系划分为两种颜色类型：两种与该国相异颜色，一种相同颜色，其中两种相异颜色具备对称性可以随意轮换，如图1，其中2和3可以轮换。

在第一次出现颜色4时，整体板块如下面示意图，由最外围国家部分边界组成的环形结构。

将外围每一段边界对应的国家分为两种：

A、只有一段边界与外围重合，此类国家的特点是该段一经被包围该国便进入“消失”行列（原则1）

B、有两段或两段以上边界与外围重合，此类国家的特点是在两段或两段以上边界的中间形成封闭区域，内部与该国相异的两种颜色具备对称性，可以自由互换（原则5）
下面对各种情况进行分类：

引理1：对于B类国家形式的封闭区域，其内部的其它B类国家由于无法跨越封闭区域，只能在内部形成形状类似的新的封闭区域，最终形态是以中间一段区域作为分界，两侧相对独立的波纹状分布，如图6，对于处于同一侧的所有B类国家而言，由中间向两侧，相邻B类国家又构成新的封闭区域，以右侧为例，由中间向右依次设为T1、T2……Tn，根据原则5与进行如下操作：在保证T1颜色不变的情况下

若Tn,Tn+1同色，则Tn+1保持颜色不变；

若Tn,Tn+1异色，但Tn+1并非第三种颜色；则Tn+1保持颜色不变；

若Tn,Tn+1异色，且Tn+1是第三种颜色，根据原则5，将Tn+1变换为与Tn相异的另一种颜色，同时每次变色后，相应封闭区域内的其它“消失”国家也要进行相应变色。

结论：对于同侧形成波纹状分布的所有B类国家在保证靠中间一侧的B类国家颜色不变的前提下，再选择边界三种颜色与B相异色的两种颜色中任一种，即可完成对同侧所有B类国家染色，且保持总体使用颜色数仍为3。

即在T1颜色不变下再任选另外两种颜色中的任一种可保证在整体板块不使用颜色4的前提下，完成对同侧所有B类国家的重新染色。

其中两种颜色必须包括T1颜色，可知，同侧的所有B类国家，可以用两种颜色即可涂色，引理完毕。

①1.2之间存在3，若3全部为A型，则4与3互换即可，若3有部分B型，则进入下一步。

②1.3之间若不存在2，则2必在右侧封闭区域内（为了3确认此情况，根据原则5的对称性，将2换作1）若右侧封闭区域仍有B类国家，则根据引理1，用3.1两颜色将全部B类国家标记。

这时2有两种可能：

①2为A型，则2与4互换即可。

②2被1.3两种颜色替换，这时整个边界已经没有2，所以不需要第四种颜色，即这时已不属于“不得不用4色”的前提。

1.3之间若存在2，且所有2均对应A类国家，那么将③内封闭区域内1.2互换，若右侧封闭区域仍有B类国家，则根据引理1，用3、1两种颜色将全部B类国家染色，这时可以确认封闭区域内无颜色2的B类国家，然后再4与所有2互换，4消失即可得到3色地图。

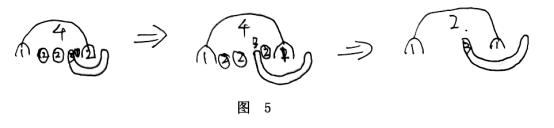
1.3之间若存在2，且2有部分或整体为B类，2的B类国家分为左侧或右侧。

若2左侧，侧2替代1的位置，继续讨论2、3之间是否存在1的情况重复上述①②步骤。

若2在右侧，则2替代3的位置，继续讨论1、2之间是否存在1的情况重复上述①②步骤。

①②得出规律推广到普遍情况。

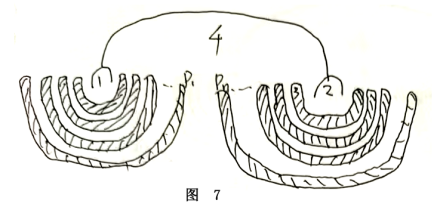
①……若P1,Pn之间存在与P1、Pn相异的颜色，且全部为A型设为Pm，将左右侧的封闭区域分别用P1,Pn的颜色为所有B型，重新涂色（引理1），保证两侧封闭区域内的Pm颜色均为A型，同时用如下方式将两端点颜色替换为P1或Pn：若最内圈B类国家与端点同色，则端点颜色即为P1或Pn保持不变。若最内圈B类国家与端点异色，则将端点替换为轮换颜色（原则5）例如若P1与2异色，则将2替换为Pn。再用4与Pm颜色互换。

②……若P1,Pn之间不存在与P1、Pn相异的颜色，则该相异颜色必在两侧封闭区域内，根据引理1再次将两侧所有B型重新涂色（用P1、Pn的颜色），这时Pm如果仍存在那么一定是A型，同时用如下方式将两端点颜色替换为P1或Pn：若最内圈B类国家与端点同色，则端点颜色即为P1或Pn保持不变。若最内圈B类国家与端点异色，则将端点替换为轮换颜色（原则5）例如若P1与2异色，则将2替换为Pn。用4与Pm，颜色互换即可，反之如果已经不存在Pm，那说明Pm已经被P1或Pn颜色取代，同时用如下方式将两端点颜色替换为P1或Pn：若最内圈B类国家与端点同色，则端点颜色即为P1或Pn保持不变。若最内圈B类国家与端点异色，则将端点替换为轮换颜色（原则5）例如若P1与2异色，则将2替换为Pn。那么“不得不用4”的前提已经不存在。

若P1、Pn之间存在P1、Pn相异的颜色，且有B型，设为Pm，若Pm位于左侧，则Pm、Pn取代之前的P1、Pn，若Pm位于右侧，则P1、Pm取代之间的P1、Pn，重复之前的操作，直至出现①或②的情况。

若最后仍未出现①②的情况，则如图9根据引理1左侧所有B型用Pn、Pm的颜色重新染色，右侧用Pm、Pn颜色重新颜色，这时P1颜色的B型全部被替代，同时用如下方式将两端点颜色替换为Pm或Pn：若最内圈B类国家与端点同色，则端点颜色即为Pm或Pn保持不变。若最内圈B类国家与端点异色，则将端点替换为轮换颜色（原则5）例如若Pm与2异色，则将2替换为Pn。将4与P1颜色替代即可。

以上证明是以二段边界，并且二段边界分布在端点两侧的情况作为范例代表所有B类国家，至于二段边界完全在两端点之内，或者拥有三段以上边界分布在端点两侧，并且有两段以上位于两端点之内的情况，同样可将位于端点之内的二段之间的封闭区域，视作独立于整体之外的部分，先当作“消失”待完成了二段边界的着色，再探讨内部即可。如下：

先将3的封闭区域视作“消失”，简单当3的整体国家，按照上述步骤证明后，再二次对3内部二次染色即可（原则5）

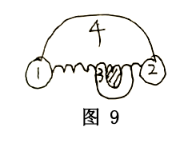
先将3的左侧封闭区域视作“消失”，当作3的二段B类国家，按照之前的方法证明后，再一次对阴影区域涂色。

以上证明，若将两端点换为同色，同理可以得到相同结果。

综上，一旦板块最外圈颜色数达到4，永远都可以通过变换，将板块最外圈颜色数重新降为3，亦即板块可以以任何一种方式无限扩展，这对应了已知的和未知的所有地图。

作者：党珅